N皇后问题的回溯算法

问题简介

首先介绍八皇后问题，八皇后问题以国际象棋作为背景，问题的描述是如何在8x8的棋盘中放下8个皇后，使得这8个皇后互相不攻击。皇后的攻击规则是同一行、列或斜线上，也就是说，要在8x8的棋盘上放8个点使得这8个点没个点在行、列、对角线上都不会有第二个点。

而N皇后问题就是八皇后问题的推广，在NxN的棋盘中放置N个点，使得这N个点互相之间无法攻击。

这只是八皇后问题的其中一个解，我们的目的是通过编程将给定的N皇后问题的所有解不重不漏的列举出来。

关于回溯

回溯法（Backtraking）是一种通过试错遍历所有可能性的方法，当问题遇到错误或无法继续的时候，回退到上一个做出选择的步骤重新选择，通过尝试所有的可能性找到问题的答案。N皇后问题就是回溯的典型应用。

问题分析

我们要解决N皇后问题，首先可以从较为容易的四皇后问题入手，四皇后问题是规模最小的存在有意义解的皇后问题。

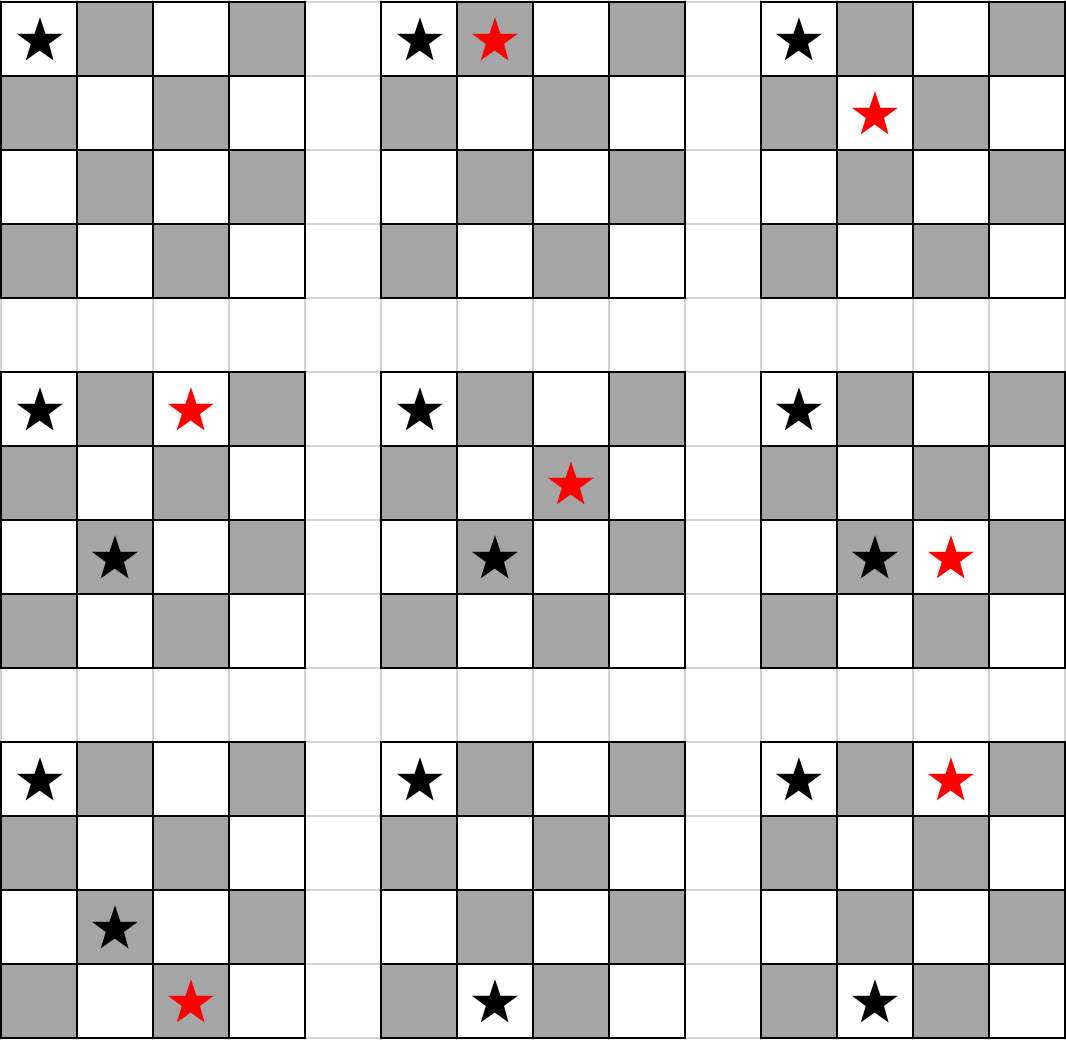
首先我们将第一个皇后放在左上角第一个格子中，由于它是第一个进入棋盘的，没有另外一个皇后与其冲突。考虑到皇后会攻击同一列同一行，所以一列中只可能有一个皇后，我们不需要考虑两个皇后在同一列的问题，直接将第二个皇后放到第二列第一个位置，由于与第一个皇后在同一行，所以这个位置不能放。然后将其往下移直至不与之前放入的皇后位置冲突时，放入第三个皇后位于第三列第一个位置（对应插图中第4个棋盘），同样的，通过判定条件一直将其往下移动。

但此时我们发现，第三个皇后无论是放在哪一个位置，都与之前放入的皇后位置冲突，此时将第三个皇后撤回，第二个皇后继续向下移动寻找下一个不冲突的位置（对应插图中第7、8两个棋盘），这个过程便是回溯。

当一个皇后无法在一整列中寻找到一个不冲突的位置的时候，回退到上一个皇后寻找下一个不冲突的位置，如果上一个皇后也已抵达列尾，则撤回上一个皇后，回退到上上一个皇后，以此类推。

代码实现思路

首先我们解决皇后的位置存储问题，以上图第9个棋盘为例，第一个皇后位于(1,1)，第二个皇后位于(4,2)，第三个皇后位于(1,3)。我们可以观察到，第N个皇后的列标总是N，故我们可以简记为第一个皇后位于1，第二个皇后位于4，第三个皇后位于1，使用一个一维数组对每一个皇后的位置进行储存，数组的下标N表示第N+1个皇后，这个下标存储的数表示我们简记的位置。

我们使用循环从第0列遍历到当前正在操作的皇后的前一列进行遍历来寻找是否有与当前皇后位置冲突的皇后，简单的比较对应的数组值就可以知道是否在同一行。判断是否位于同一对角线需要两个判断条件，对于从左上到右下方向的对角线，两个位置的行标差等于列标差的话，即在一条对角线上；对于从左下到右上方向的对角线，两个位置的行标和与列标和相当。通过这三个判断条件，我们可以对比两个坐标是否满足皇后问题的要求。

如果我们在循环遍历检测皇后位置是否冲突的过程中发现有冲突的皇后，则当前操作的皇后向下移动一位。这里又要区分两个区别，如果向下移动后还没越出棋盘边界，则需要重新遍历检测新的位置是否冲突；如果已经越界，说明当前操作的皇后已抵达棋盘边界，需要撤出棋盘，返回上一个皇后进行回溯。

我们还需要另一个循环来依此操作每一个皇后，这个循环每循环一次，便意味着有一个皇后已经放到正确的位置上了。

当这个循环结束后，数组中存储的位置便是皇后问题的其中一个解。那么如何才能输出所有的解呢？我们在结束循环后将最后一列的皇后向下移动一位，破坏棋盘的平衡，然后重新进行以上操作继续回溯便能找出所有的解。

N皇后问题的难点其实在于边界条件的判定，如果边界条件不清晰，就很容易出现数组越界的情况，下面给出代码实现。

void queenQuestionSolution(int numberOfQueen){
    int[] queenPosition = new int[numberOfQueen];
    int numberOfSolutions = 0;
    while(true){
        for (int i = 0; i < numberOfQueen; i++){
            for (int n = 0; n < i; n++){
                if (queenPosition[n] == queenPosition[i] ||
                        queenPosition[n] - queenPosition[i] + n - i == 0 ||
                        queenPosition[n] - queenPosition[i] == n - i ||
                        queenPosition[i] >= numberOfQueen){
                    queenPosition[i]++;
                    if(queenPosition[i] < numberOfQueen){
                        n = -1;
                    }
                    else{
                        queenPosition[i] = 0;
                        if(i == 1 && queenPosition[i - 1] == numberOfQueen - 1) {
                            System.out.println("Without Solution or All Solutions have been found.");
                            return;
                        }
                        else
                            queenPosition[i - 1]++;
                        i--;
                        n = -1;
                    }
                }
            }
        }
      
        System.out.println("No." + ++numberOfSolutions + " Solution of " + numberOfQueen + " Queen Question");
        for (int i = 0; i < numberOfQueen; i++){
            for (int j = 0; j < numberOfQueen; j++){
                if (queenPosition[j] == i)
                    System.out.print("# ");
                else
                    System.out.print("0 ");
            }
            System.out.println("");
        }
        queenPosition[numberOfQueen - 1] ++;
    }
}